Princeton Review
"1,012 GMAT Practice Questions"
Standard Deviation Drill (page 239)
-data sufficiency question
8. If set S consists of an odd number of even integers that have a normal distribution, what is the standard deviation of set S?
(1) The mean of set S is 4.
(2) The median of set S is 4.
--------------------------------------------------------------------------------
Book Answer: (C)
"Statement (1) is not sufficient because it tells you the mean, but nothing about the other numbers in the set. You could Plug In two sets of numbers for the set and get two different standard deviation. Eliminate choices (A) and (D). Statement (2) is also insufficient. Again, you could Plug In two sets of numbers to get two different standard deviations. Eliminate choice (B). Combining the two statements tells you that the numbers in set S are consecutive, because in a consecutive set of numbers, the mean equals the median. If the numbers are consecutive, even integers and the mean is 4, you know that the standard deviation is 2."
--------------------------------------------------------------------------------
I agree that the only possible choices are (C) or (E). But! Why must the set be consecutive? For example, consider this set of even numbers,
{4, 6, 10, 12, 18}
The mean and median are both 10 yet the set is not consecutive. Correct? I thought for a set to be consecutive there had to be even spacing between numbers that were in ascending or descending order. Like:
{3,4,5,6,7,8} or {-5,-4,-3,-2,-1,0,1,2,3}
Are the following considered consecutive number sets?
{5,10,15,20,25} or {-80, -84, -88, -92}
One last question:
Assume that the set in the book question is consecutive with a mean of 4, just like the author concluded in the answer. Why must the standard deviation be 2? The set could be ANY size. The only restrictions are that there are "an odd number of even integers." If there were 25 even, consecutive integers with a mean of 4, the standard deviation would surely not be 2! Therefore the information is insufficient and the answer is choice (E).
--------------------------------------------------------------------------------
Did I do everything right? Can you please explain consecutive number sets more clearly? Did I come to the correct conclusion?
GMAT Forum
7 postsPage 1 of 1
- thouldin
- Students
- Posts: 2
- Joined: Thu Oct 01, 2009 3:38 am
- helloriteshranjan
- Students
- Posts: 30
- Joined: Tue Aug 25, 2009 12:40 am
Re: If set S consists of an odd number
consecutive even numbers implies equally spaced consecutive numbers.
Standard deviation :
The square root of the sample variance of a set of N values is the sample standard deviation
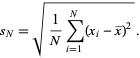
where Xi is ith member of set
x with bar over head is mean of the set.
the expression above is taken off from http://mathworld.wolfram.com/StandardDeviation.html
since the difference between the mean , 4 in this case, and other consecutive numbers, like for example the set be [-4,-2,0,2,4,6,8,10,12] will be a multiple of 2, not exactly 2. when we square them , sum them and divide the sum by the number of members,which is 9
we get Std Dev = sqrt(240/9)=5.16
which is not 2 definitely.
I think this is correct.
Standard deviation :
The square root of the sample variance of a set of N values is the sample standard deviation
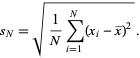
where Xi is ith member of set
x with bar over head is mean of the set.
the expression above is taken off from http://mathworld.wolfram.com/StandardDeviation.html
since the difference between the mean , 4 in this case, and other consecutive numbers, like for example the set be [-4,-2,0,2,4,6,8,10,12] will be a multiple of 2, not exactly 2. when we square them , sum them and divide the sum by the number of members,which is 9
we get Std Dev = sqrt(240/9)=5.16
which is not 2 definitely.
I think this is correct.
- jerly_vivek
- Students
- Posts: 19
- Joined: Thu Jun 04, 2009 5:58 pm
Re: If set S consists of an odd number
The set {4, 6, 10, 12, 18} does not follows normal distribution, i.e. the well known bell shaped curve. In normal distribution the bigger values lies in the centre.
- helloriteshranjan
- Students
- Posts: 30
- Joined: Tue Aug 25, 2009 12:40 am
Re: If set S consists of an odd number
jerly_vivek Wrote:The set {4, 6, 10, 12, 18} does not follows normal distribution, i.e. the well known bell shaped curve. In normal distribution the bigger values lies in the centre.
i think its "mean" not "bigger"
- Ben Ku
- ManhattanGMAT Staff
- Posts: 817
- Joined: Sat Nov 03, 2007 7:49 pm
Re: If set S consists of an odd number
thouldin Wrote:Book Answer: (C)
"Statement (1) is not sufficient because it tells you the mean, but nothing about the other numbers in the set. You could Plug In two sets of numbers for the set and get two different standard deviation. Eliminate choices (A) and (D). Statement (2) is also insufficient. Again, you could Plug In two sets of numbers to get two different standard deviations. Eliminate choice (B). Combining the two statements tells you that the numbers in set S are consecutive, because in a consecutive set of numbers, the mean equals the median. If the numbers are consecutive, even integers and the mean is 4, you know that the standard deviation is 2."
--------------------------------------------------------------------------------
I agree that the only possible choices are (C) or (E). But! Why must the set be consecutive? For example, consider this set of even numbers,
{4, 6, 10, 12, 18}
The mean and median are both 10 yet the set is not consecutive. Correct? I thought for a set to be consecutive there had to be even spacing between numbers that were in ascending or descending order. Like:
I propose that the question is written poorly, and the explanation is incorrect.
The conclusion that's drawn in the explanation to the question is incorrect. While it's correct that in any evenly-spaced (therefore consecutive) set of numbers, the mean = median, the converse is not true: just because mean=median does not mean the set consists of evenly spaced.
When there is a question about standard deviation, it's asking about how spread out the distribution is. Both statements tell us about the middle of the distribution, but not about the spread. The answer should be (E).
Finally, when the distribution is "normal," by definition, the mean = median. So (C) doesn't tell us anything we don't already know.
Hope that clears things up.
Ben Ku
Instructor
ManhattanGMAT
Instructor
ManhattanGMAT
- poonamchiK
- Students
- Posts: 103
- Joined: Tue Dec 22, 2009 3:16 am
Re: If set S consists of an odd number
I agree that statement 1 and 2 put together still leave us hanging. I had plugged in a few nos. and i get the answer E myself.
Bt since the book answer and GMAT answer is c, wont we lose a mark in this?
Poonam
Bt since the book answer and GMAT answer is c, wont we lose a mark in this?
Poonam
- RonPurewal
- Students
- Posts: 19744
- Joined: Tue Aug 14, 2007 8:23 am
Re: If set S consists of an odd number
yeah. wow, this question is just awful, in every conceivable way.
it's also impossible for a finite set of integers to "have a normal distribution". (a normal distribution - which is NOT TESTED on the gmat, by the way - is only possible if there are infinitely many data points. if the set of data is finite, they can approximate a normal distribution, but they can't actually have one.)
...and there's also the other blatant error, pointed out above by ben ku.
it's also impossible for a finite set of integers to "have a normal distribution". (a normal distribution - which is NOT TESTED on the gmat, by the way - is only possible if there are infinitely many data points. if the set of data is finite, they can approximate a normal distribution, but they can't actually have one.)
...and there's also the other blatant error, pointed out above by ben ku.
7 posts Page 1 of 1