Q10

[kmewmewblue]

How do I do this? Any advice, please?

[timmydoeslsat]

This is my diagram:



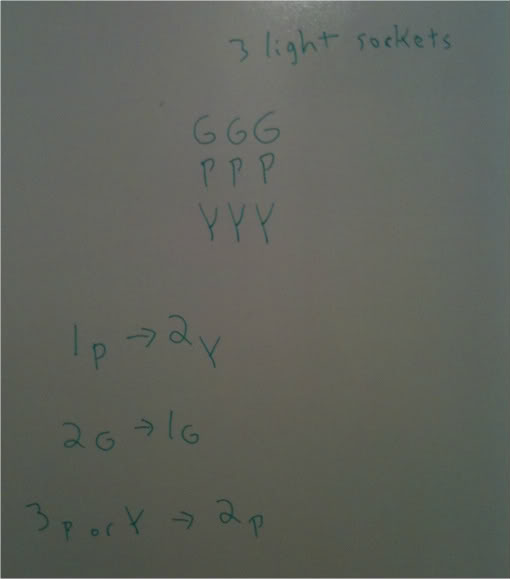
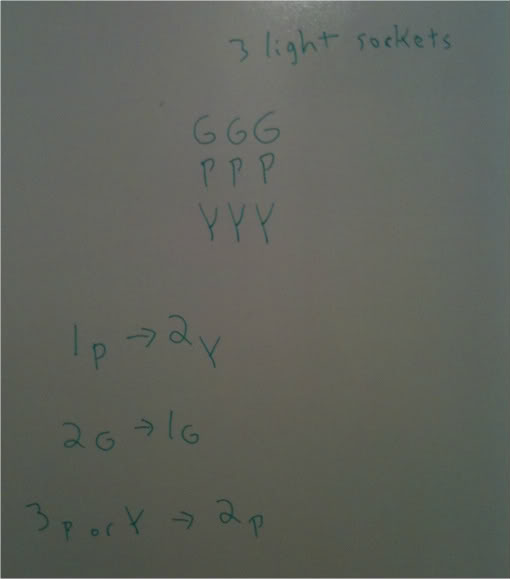
The important aspect of this diagram is really the conditional rules.

Before we get to the rules, we know that we have three light sockets. We also know that we have an ample amount of bulbs. In fact, we could, as of now, before looking at the rules, run a gauntlet of straight colored bulbs, meaning 1-2-3 are all G, Y, or P.

However, the conditional rules will restrain its use.

So question 10 tells us that there are no green bulbs and we are to figure out how many different color sequences there can be. We know that each light bulb must be either P or Y.

Looking at the conditional rules will help us solve this question.

The second rule is not going to help us because we know that no light will be green.

Notice the last rule. Take note of its contrapositive. What would happen if we were to not have P in socket 2? We could not place P in socket 3 and we could no place Y in socket 3. This would leave us with G in socket 3. And since we know that cannot happen, we must have P go in socket 2.

What happens now that P is in socket 2? From the first rule, we know that its contrapositive will allow us to conclude that socket 1 is not purple. This means it must be yellow.

We now know that 1 is Y, 2 is P, and 3 is either P or Y.

At this point we want to look at our rules and see if our hand is forced into deciding which color socket 3 must have. And we do not have any rules forcing that decision. Thus, there are 2 different sequences. Either YPP or YPY.

[kmewmewblue]

timmydoeslsat, you are most kind. Thank you very much.